5.2 KiB
| aliases | tags | date | zero-link | parents | linked | |||
|---|---|---|---|---|---|---|---|---|
|
|
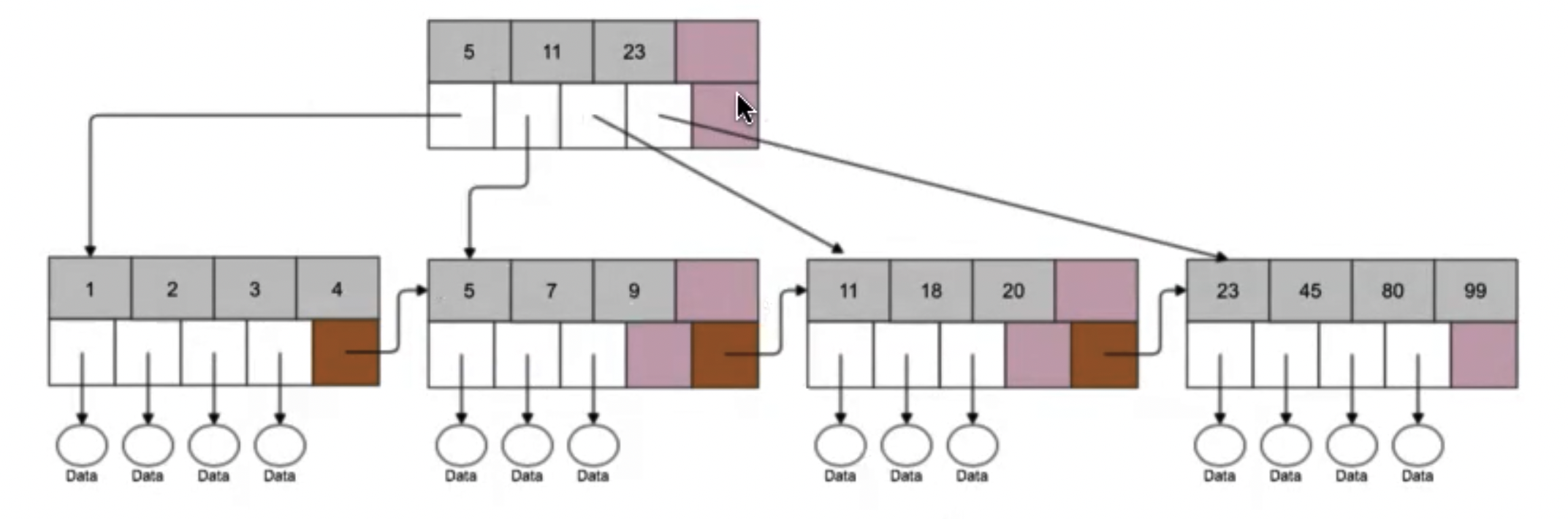
Сбалансированное сильно-ветвистое дерево. Позволяет хранить в узле множество значений.
- Узел содержит множество элементов.
- Каждый узел является по факту страничкой на диске, это позволяет уменьшить издержки на чтение с диска.
- В каждом узле есть ссылка на следующий и предыдущий узел (B+tree).
- В узлах дерева лежат либо данные, либо указатель на данные.
В таком дереве есть параметр t - минимальная степень. От этого параметра зависит, сколько будет храниться элементов в 1 узле дерева. В каждом узле должно храниться не мене t-1 ключе, и не более 2t-1. Правильно не выполняется для корневого значения.
Какое t использовать?
- Больше t -> меньше высота дерева
- зависит от размера блока на диске
- зависит от объема ОЗУ
- Обычно t выбирается от 50 до 2000.
- t = 1001 и 1 млрд. записей => 3 операции для любого ключа
Элементы в узле бинарного дерева отсортированы.
Большое количество элементов в узле позволяет делать деревья с большим количеством элементов, но с небольшой высотой.
С чем может помочь:
- Поиск по равенству (a=5)
- Поиск по открытому диапазон (a > 5 или a < 3)
- Поиск по закрытому диапазону (3 < a < 8)
- LIKE тоже работает с индексами, но только по префиксам
- LIKE 'a%' - хорошо
- LIKE '%c' - плохо С чем НЕ поможет:
- Искать четные/нечетные числа
- Искать суффиксы. LIKE '%c' - плохо
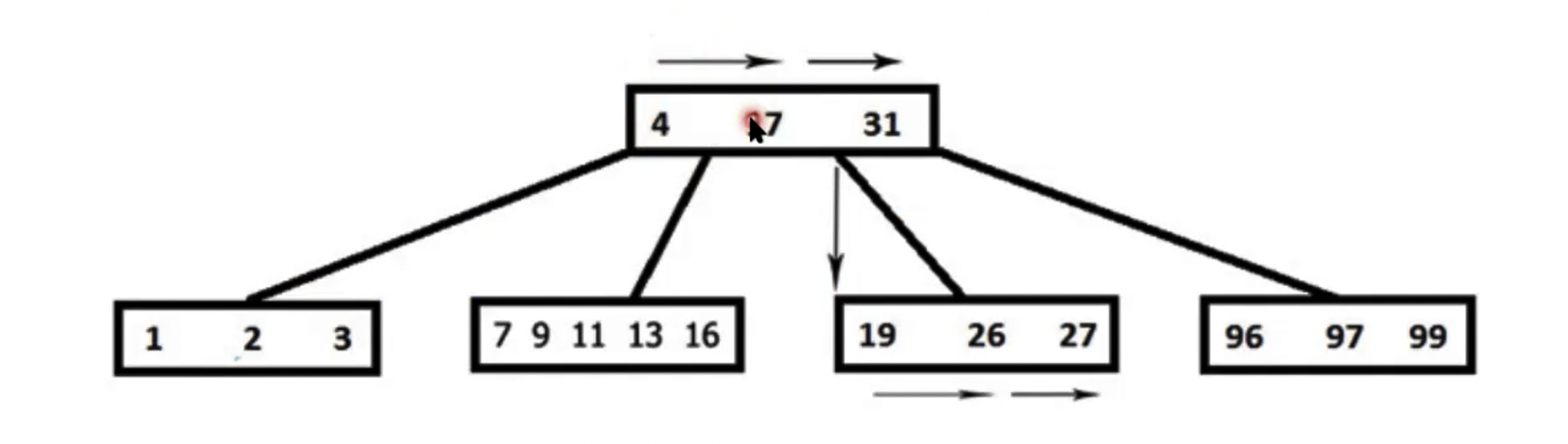
Поиск в B-tree
Пример поиска 27.
Важно. Значения в узлах могут быть не уникальными. Например, могло быть 2 числа 27. В таком случае поиск продолжается. При этом стоит учитывать, что количество элементов внутри узла ограничено, а значит следующий элемент (27) может находится в следующем узле. Поэтому для оптимизации этой проблемы блоки на одном уровне линкуют, создавая связный список, чтобы легко перейти в следующий блок.
- алгоритм аналогичен бинарному дереву, но выбор не из 2-ух, а из нескольких
- поиск за O(t logt(n))
- Но обращений к диску O(logt(n))
Добавление в B-tree
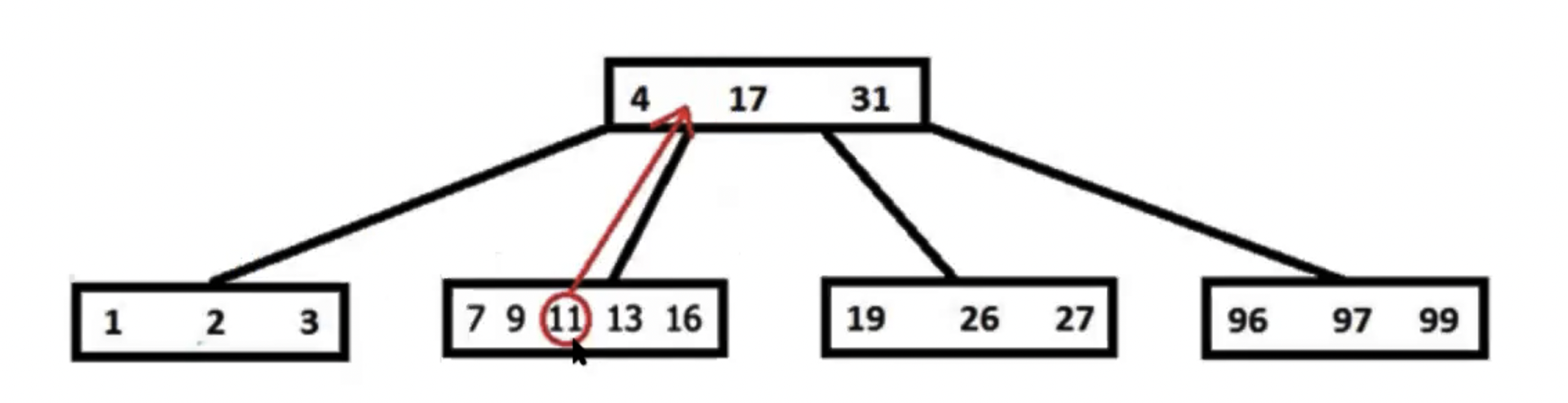
Представим, что у нас уже есть вот такое дерево, и нам надо вставить в него значение 15
Мы понимаем, что вставка должна быть между 4 и 17, там у нас есть узел 7...16. Но в него мы вставить не можем, так как в данном случае у нас t = 3, а значит в блоке не должно быть больше 5 значений.
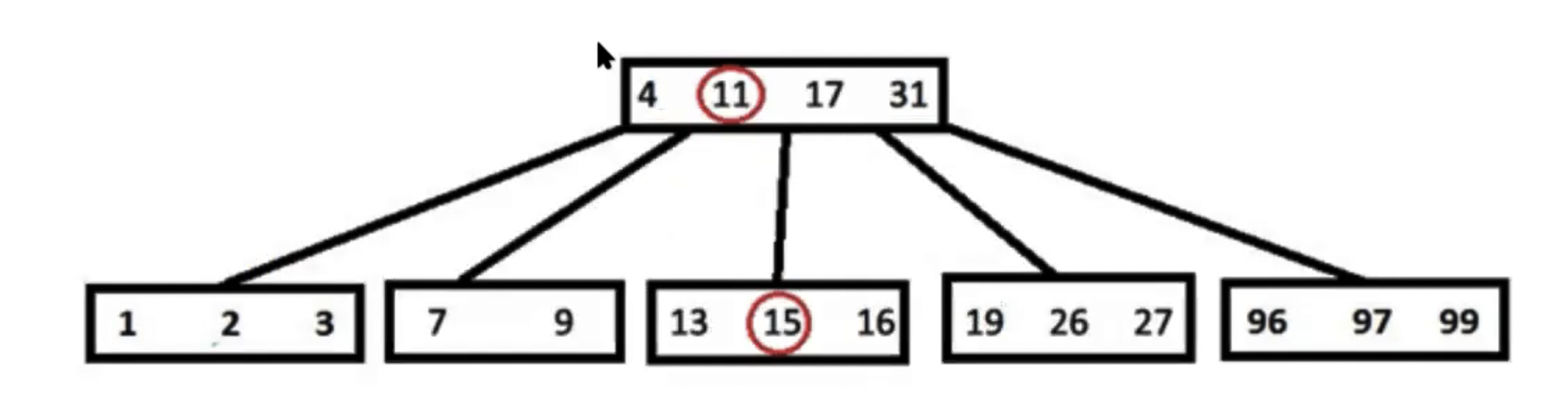
Поэтому блок разбивается начиная с t-1 элементу. В данном случае это 11. Элемент, по которому разбивается блок перемещается в родительский блок. Если в родительском блоке происходит переполнение, то родительский блок тоже разбивается и так далее.
После вставки мы получим следующее дерево
Мета информация
Область:: ../../../meta/zero/00 Разработка, ../../../meta/zero/00 Алгоритм Родитель:: Tree Источник:: Автор:: Создана:: 2024-01-29